[TS] 09. Forecast 실습

Time Series
Author

김보람

Published

December 6, 2023

options(repr.plot.width = 12, repr.plot.height = 6)

EX 8.7 모의 실험 데이터

getwd()
'/home/coco/Dropbox/Scribbling/posts' 
z <- scan("eg8_7.txt")
forecast::tsdisplay(z)
Registered S3 method overwritten by 'quantmod':
  method            from
  as.zoo.data.frame zoo

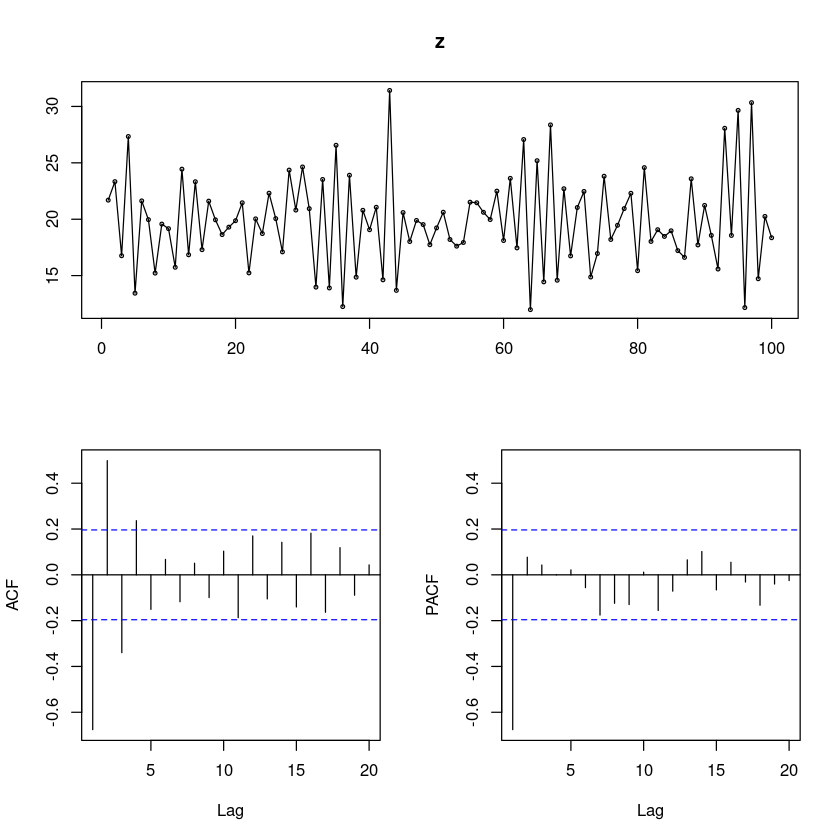
  • 평균이 20정도로 움직이는 정상 시계열로 보인다. —> AR(1)모형
forecast::ggtsdisplay(z,
        smooth=T)
`geom_smooth()` using formula = 'y ~ x'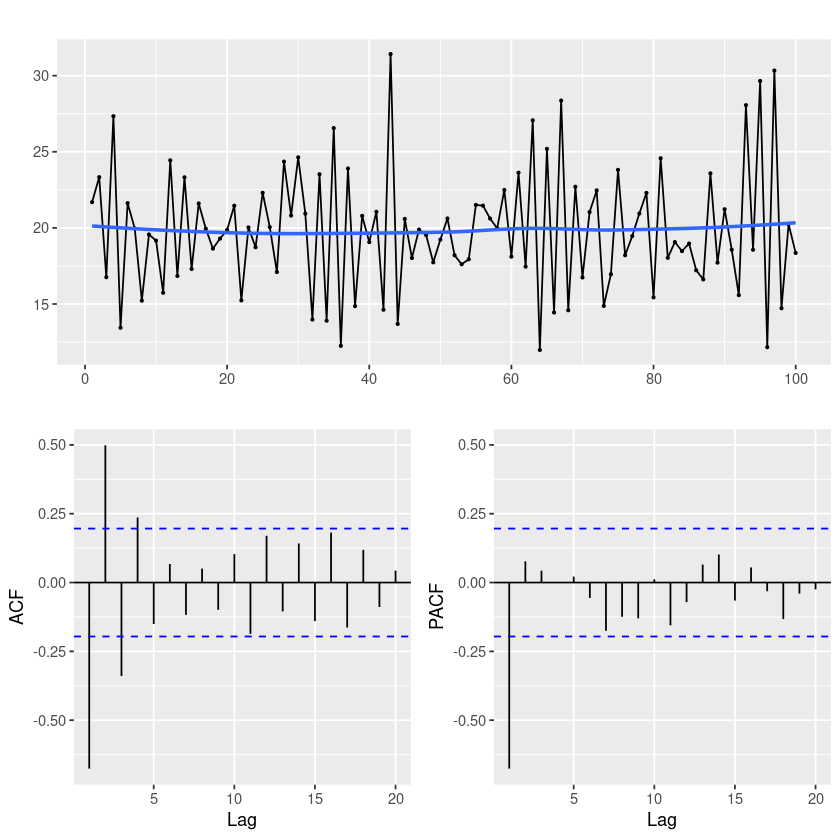

  • smooth=T를 쓰면 추세가 있는지 확인하는 파란 선이 생긴다.
fit <- arima(z, order=c(1,0,0), method='ML')
fit

Call:
arima(x = z, order = c(1, 0, 0), method = "ML")

Coefficients:
          ar1  intercept
      -0.6715    19.8312
s.e.   0.0728     0.1776

sigma^2 estimated as 8.744:  log likelihood = -250.61,  aic = 507.22
mean(z)
19.832691
  • intercept는 delta가 아니라 mu이다.

\(\hat Z_n(l) = \hat μ + \hat ϕ^l(Z_n − \hat μ)\)

length(z)
100

- 예측하는 함수

  • 모형을 기준으로 25개를 예측할거야!
forecast_fit <- forecast::forecast(fit, 25) #MMSE : zn(l) = mu + phi^l*(zn-mu), l=1,...,25
forecast_fit
    Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
101       20.82225 17.03269 24.61181 15.02662 26.61788
102       19.16558 14.60082 23.73034 12.18439 26.14678
103       20.27811 15.40393 25.15229 12.82369 27.73253
104       19.53100 14.52353 24.53847 11.87273 27.18926
105       20.03272 14.96628 25.09915 12.28427 27.78116
106       19.69579 14.60299 24.78859 11.90702 27.48456
107       19.92205 14.81740 25.02670 12.11517 27.72893
108       19.77011 14.66013 24.88009 11.95507 27.58515
109       19.87214 14.75976 24.98453 12.05343 27.69086
110       19.80362 14.69015 24.91709 11.98325 27.62399
111       19.84964 14.73568 24.96359 12.02852 27.67076
112       19.81874 14.70456 24.93291 11.99728 27.64019
113       19.83949 14.72521 24.95376 12.01788 27.66110
114       19.82555 14.71123 24.93987 12.00387 27.64723
115       19.83491 14.72057 24.94925 12.01320 27.65662
116       19.82863 14.71428 24.94297 12.00690 27.65035
117       19.83285 14.71849 24.94720 12.01112 27.65457
118       19.83001 14.71566 24.94437 12.00828 27.65174
119       19.83191 14.71756 24.94627 12.01018 27.65365
120       19.83064 14.71628 24.94499 12.00890 27.65237
121       19.83150 14.71714 24.94585 12.00976 27.65323
122       19.83092 14.71656 24.94527 12.00919 27.65265
123       19.83131 14.71695 24.94566 12.00957 27.65304
124       19.83105 14.71669 24.94540 12.00931 27.65278
125       19.83122 14.71686 24.94558 12.00949 27.65295

- 직접 계산

coef(fit)
ar1
-0.671544059932036
intercept
19.8311503070686
hat_phi <- coef(fit)[1]
hat_mu <- coef(fit)[2]
hat_mu + hat_phi * (z[100] - hat_mu) # l= 1 z_100_(1)
hat_mu + hat_phi^2 * (z[100] - hat_mu) # l= 2 z_100_(2)
intercept: 20.8222488141294
intercept: 19.1655839918444
  • 100번째를 기준으로 그 다음값을 구하고 싶어.
l <- 1:10
sapply(l, function(x) hat_mu + hat_phi^x * (z[100] - hat_mu))
intercept
20.8222488141294
intercept
19.1655839918444
intercept
20.2781074125482
intercept
19.5309989178393
intercept
20.0327151895859
intercept
19.6957906075232
intercept
19.9220503092525
intercept
19.7701069505542
intercept
19.8721436105341
intercept
19.8036214976293
plot(forecast_fit)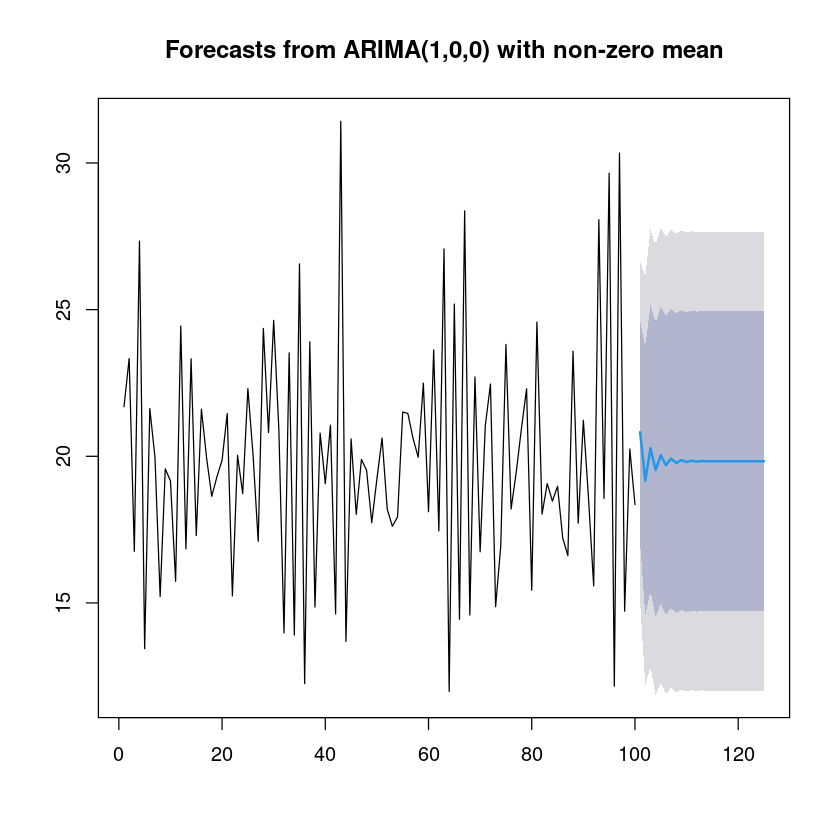

  • 점점 평균값으로 수렴한다.

  • AR process의 정보가 점점 사라지는 것..

ggplot2::autoplot(forecast_fit)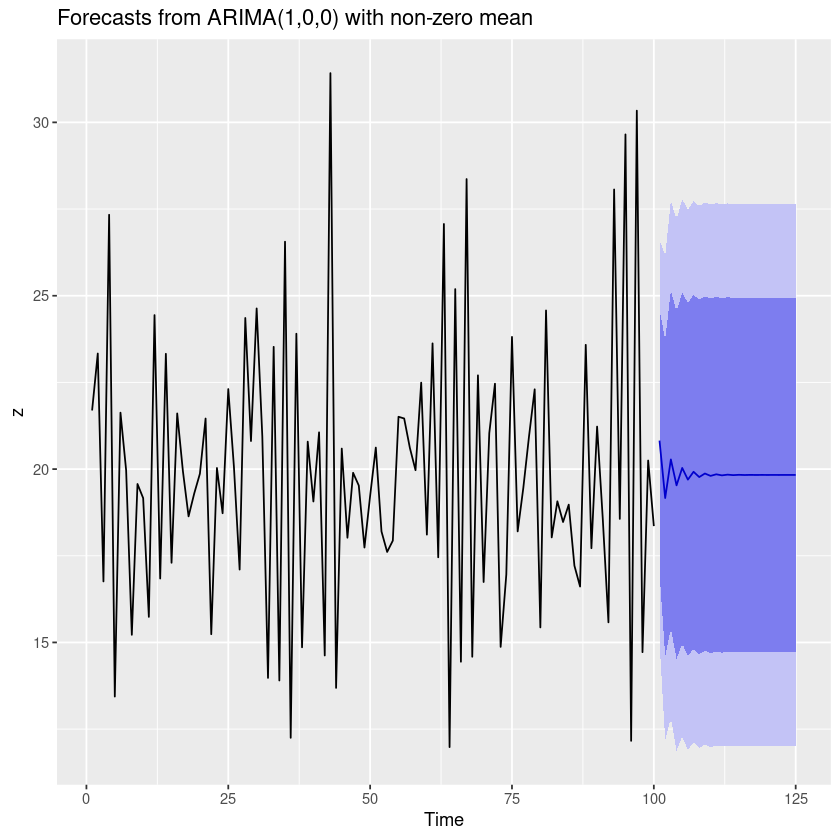

sarima_fit <- astsa::sarima.for(z,25,1,0,0)  # z함수, 25개 볼거야, p, d, q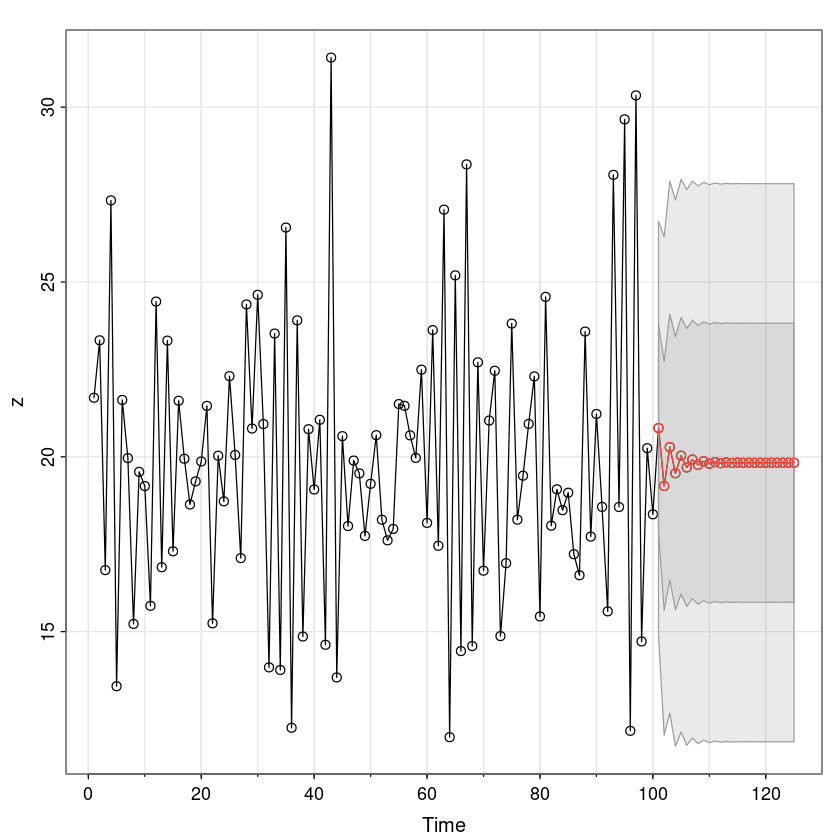

sarima_fit$pred
sarima_fit$se
A Time Series:
  1. 20.8222483489762
  2. 19.1655839559512
  3. 20.2781070098918
  4. 19.5309988141942
  5. 20.032714849742
  6. 19.6957904500696
  7. 19.9220500133516
  8. 19.7701067583474
  9. 19.8721433414928
  10. 19.8036212850204
  11. 19.849636861772
  12. 19.8187353767205
  13. 19.8394870839858
  14. 19.8255513992216
  15. 19.8349098248857
  16. 19.8286252301641
  17. 19.8328456121207
  18. 19.830011439887
  19. 19.8319147112811
  20. 19.8306365807722
  21. 19.8314949016627
  22. 19.8309185014078
  23. 19.8313055795478
  24. 19.8310456395405
  25. 19.831220200696
A Time Series:
  1. 2.95700711959937
  2. 3.5619005566917
  3. 3.80334404182832
  4. 3.90734998536685
  5. 3.95335857242263
  6. 3.97393285636323
  7. 3.98317649989949
  8. 3.98733810739122
  9. 3.98921345277822
  10. 3.99005889146209
  11. 3.99044010149264
  12. 3.9906120043846
  13. 3.99068952524303
  14. 3.99072448443737
  15. 3.99074024993262
  16. 3.99074735969909
  17. 3.990750565996
  18. 3.99075201194324
  19. 3.99075266402387
  20. 3.99075295809352
  21. 3.9907530907105
  22. 3.99075315051696
  23. 3.99075317748796
  24. 3.99075318965111
  25. 3.99075319513634
head(sarima_fit$pred + qnorm(0.975)*sarima_fit$se) ##95% 신뢰구간 상한
head(sarima_fit$pred - qnorm(0.975)*sarima_fit$se) ##95% 신뢰구간 하한
A Time Series:
  1. 26.6178758054195
  2. 26.1467807635801
  3. 27.7325243526903
  4. 27.1892640605063
  5. 27.781155269663
  6. 27.4845557255219
A Time Series:
  1. 15.0266208925329
  2. 12.1843871483223
  3. 12.8236896670933
  4. 11.8727335678821
  5. 12.2842744298209
  6. 11.9070251746172

EX 9.5 IMA(1,1) = ARIMA(0,1,1)

  • 차분을 했더니 MA(1)모형
z <- scan("eg9_5.txt")
forecast::ggtsdisplay(z, smooth=T)
`geom_smooth()` using formula = 'y ~ x'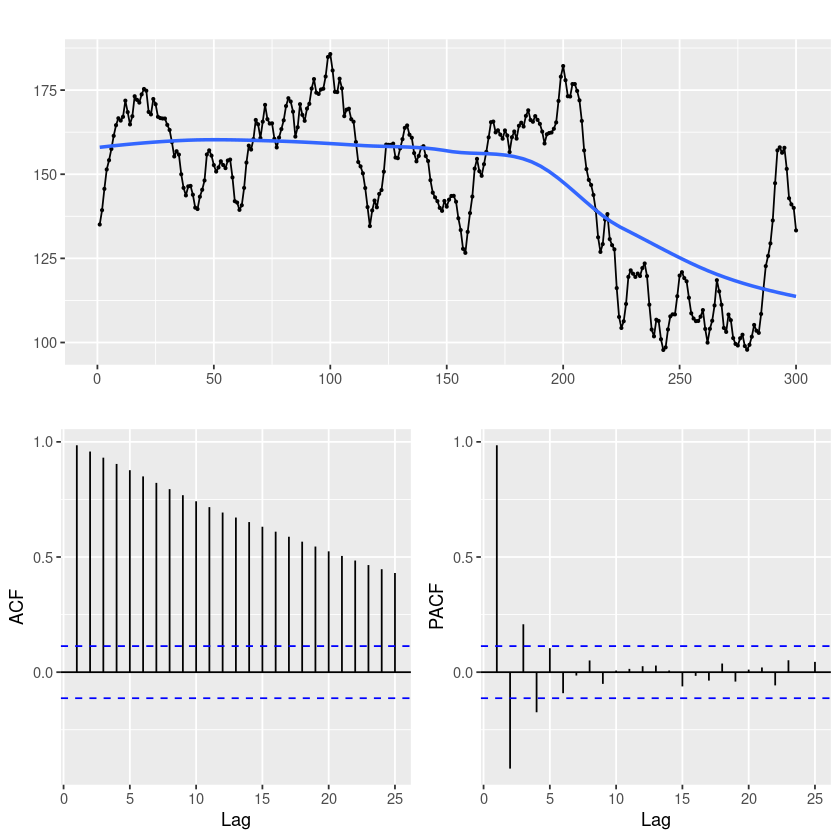

  • ACF가 천천히 감소한다. (확률적 추세가 있어보임)
##단위근 검정 : H0 : 단위근이 있다.
fUnitRoots::adfTest(z, lags = 0, type = "c")
fUnitRoots::adfTest(z, lags = 1, type = "c")
fUnitRoots::adfTest(z, lags = 2, type = "c")

Title:
 Augmented Dickey-Fuller Test

Test Results:
  PARAMETER:
    Lag Order: 0
  STATISTIC:
    Dickey-Fuller: -1.43
  P VALUE:
    0.5246 

Description:
 Tue Dec  5 20:19:59 2023 by user: 

Title:
 Augmented Dickey-Fuller Test

Test Results:
  PARAMETER:
    Lag Order: 1
  STATISTIC:
    Dickey-Fuller: -2.3543
  P VALUE:
    0.1803 

Description:
 Tue Dec  5 20:19:59 2023 by user: 

Title:
 Augmented Dickey-Fuller Test

Test Results:
  PARAMETER:
    Lag Order: 2
  STATISTIC:
    Dickey-Fuller: -1.7307
  P VALUE:
    0.4126 

Description:
 Tue Dec  5 20:19:59 2023 by user:

  • 평균이 있으니 ‘C’ 옵션을 사용하자.

  • 모든 차수에 대해서 p-value < 0.05이므로 차분이 필요하다.

lag_z <- diff(z)
forecast::tsdisplay(lag_z)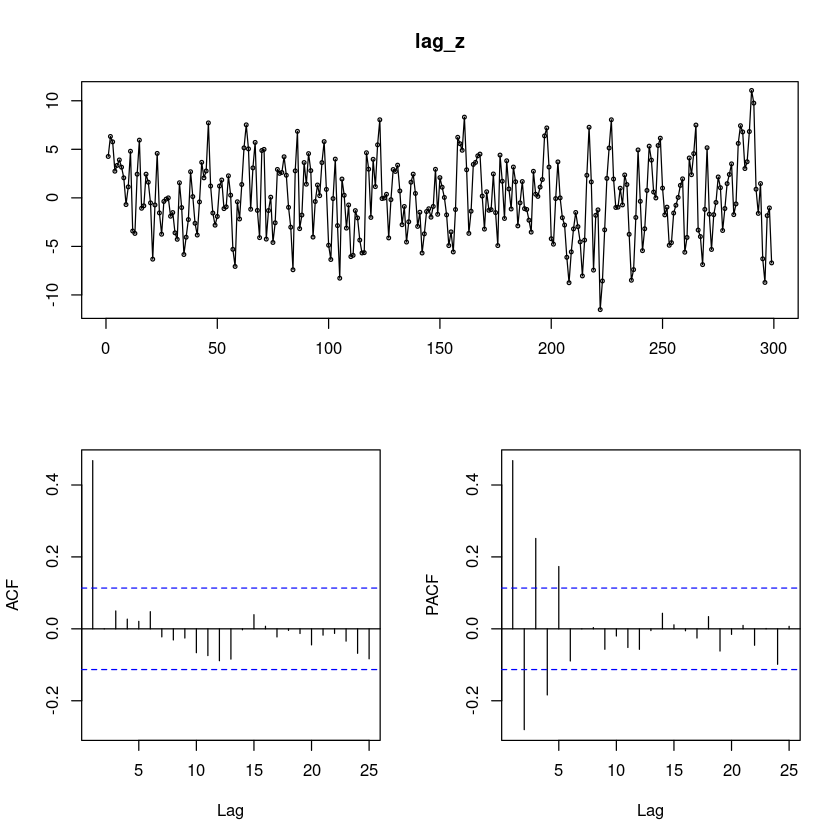

  • 0을 중심으로 움직인다.

  • PACF가 SIN함수를 그리며 지수적으로 감소함

  • ACF가 1차에만 유효하고 나머지는 유효하지 않음 -> MA(1)모형

## mean : H0 : mu = 0
t.test(lag_z)

    One Sample t-test

data:  lag_z
t = -0.02617, df = 298, p-value = 0.9791
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.4480209  0.4362617
sample estimates:
   mean of x 
-0.005879599
  • 유의확률이 크게 나와서 평균이 0이 맞아!

- 차분한 모형(평균 F)

fit1 <- arima(lag_z, order=c(0,0,1), include.mean = F)
fit1

Call:
arima(x = lag_z, order = c(0, 0, 1), include.mean = F)

Coefficients:
         ma1
      0.7605
s.e.  0.0342

sigma^2 estimated as 9.479:  log likelihood = -760.93,  aic = 1525.86

- 원래 모형(평균 있음)

fit <- arima(z, order=c(0,1,1))
fit

Call:
arima(x = z, order = c(0, 1, 1))

Coefficients:
         ma1
      0.7605
s.e.  0.0342

sigma^2 estimated as 9.479:  log likelihood = -760.93,  aic = 1525.86
  • 두 가지 방법이 모두 동일하게 나온다.

\(Z_t = ε_t + 0.7605ε_t, \hat θ = −0.7605\)

  • 부호가 반대!!!

  • MA모형 평균이 없당

- 잔차분석

forecast::checkresiduals(fit)

    Ljung-Box test

data:  Residuals from ARIMA(0,1,1)
Q* = 7.1117, df = 9, p-value = 0.6255

Model df: 1.   Total lags used: 10

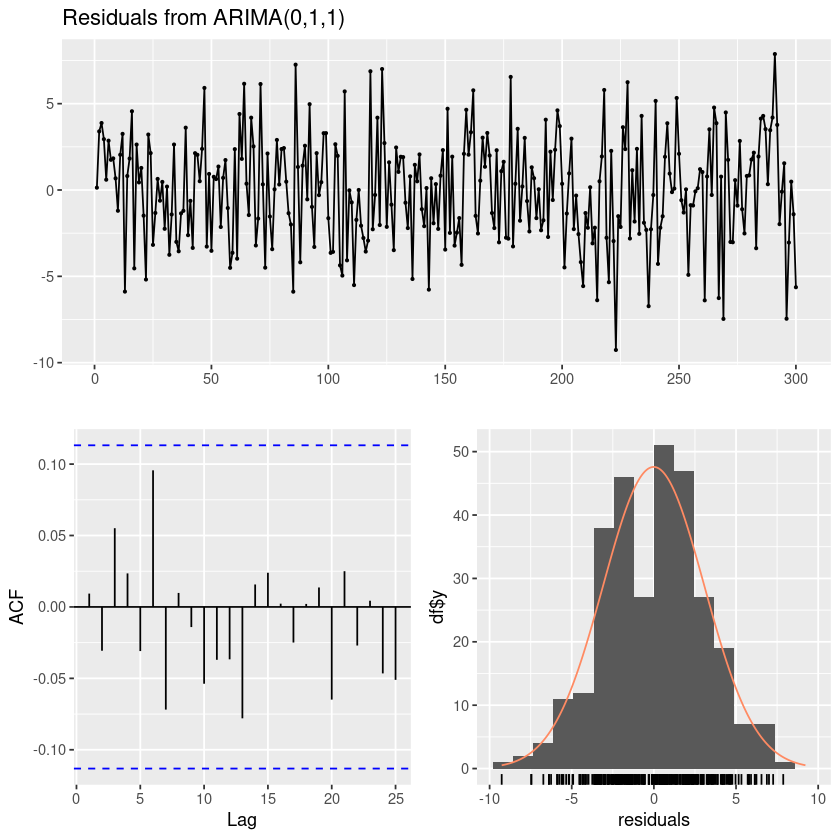
  • 정규분포

  • 10개시차까지 모든 cov가 0

  • WN이다

resid = resid(fit)
forecast::tsdisplay(resid)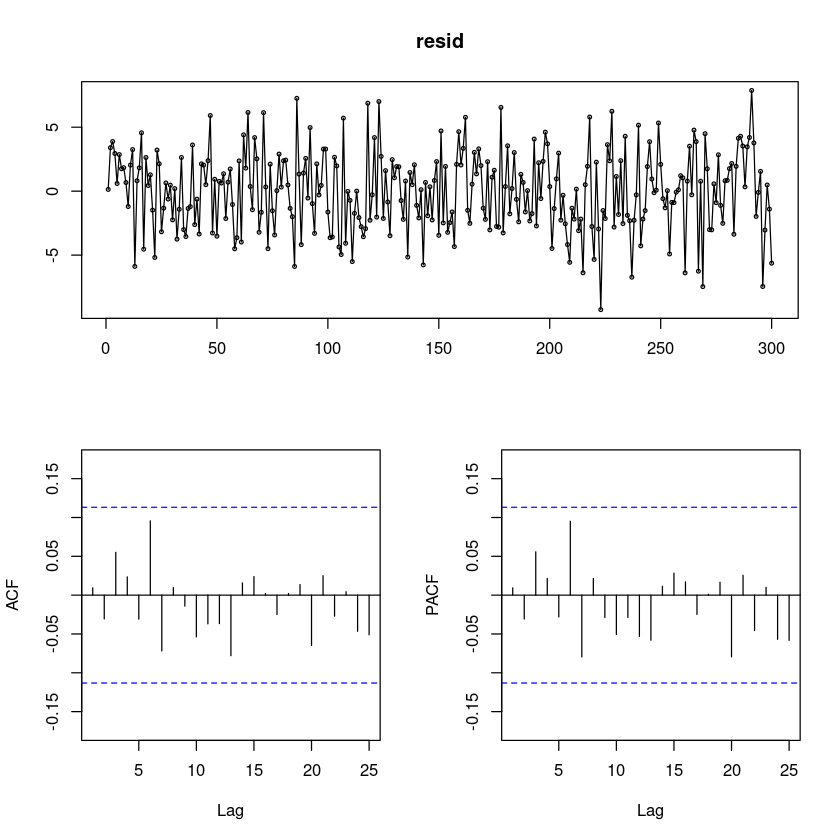

# 잔차의 포트맨토 검정 ## H0 : rho1=...=rho_k=0
portes::LjungBox(fit, lags=c(6,12,18,24))
A matrix: 4 × 4 of type dbl
lags statistic df p-value
6 4.520231 5 0.4771812
12 7.964175 11 0.7165093
18 10.346863 17 0.8884381
24 12.926680 23 0.9535620 
## 정규성검정
tseries::jarque.bera.test(resid) ##JB test H0: normal

    Jarque Bera Test

data:  resid
X-squared = 1.1606, df = 2, p-value = 0.5597
par(mfrow=c(1,2))
hist(resid)

qqnorm(resid, pch=16)
qqline(resid)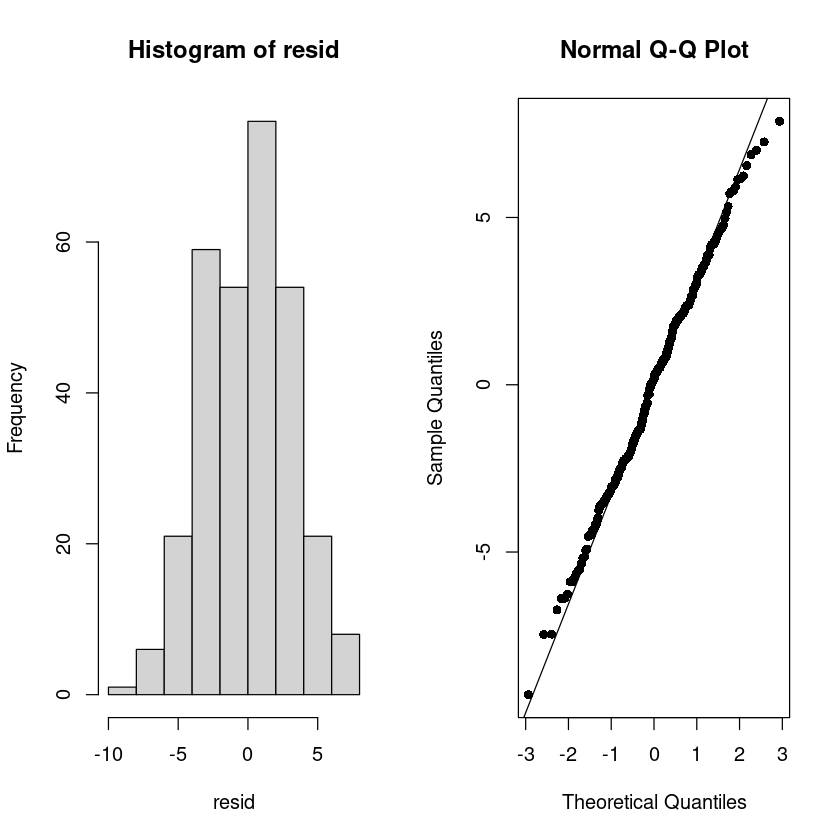

## 잔차 검정
astsa::sarima(z, p=0, d=1, q=1)
initial  value 1.355425 
iter   2 value 1.182804
iter   3 value 1.144176
iter   4 value 1.129179
iter   5 value 1.127095
iter   6 value 1.125914
iter   7 value 1.125753
iter   8 value 1.125727
iter   9 value 1.125726
iter  10 value 1.125726
iter  11 value 1.125726
iter  11 value 1.125726
final  value 1.125726 
converged
initial  value 1.125981 
iter   2 value 1.125979
iter   3 value 1.125977
iter   4 value 1.125975
iter   5 value 1.125974
iter   6 value 1.125974
iter   6 value 1.125974
final  value 1.125974 
converged
$fit

Call:
arima(x = xdata, order = c(p, d, q), seasonal = list(order = c(P, D, Q), period = S), 
    xreg = constant, transform.pars = trans, fixed = fixed, optim.control = list(trace = trc, 
        REPORT = 1, reltol = tol))

Coefficients:
         ma1  constant
      0.7605   -0.0146
s.e.  0.0342    0.3130

sigma^2 estimated as 9.479:  log likelihood = -760.93,  aic = 1527.86

$degrees_of_freedom
[1] 297

$ttable
         Estimate     SE t.value p.value
ma1        0.7605 0.0342 22.2124  0.0000
constant  -0.0146 0.3130 -0.0468  0.9627

$AIC
[1] 5.109891

$AICc
[1] 5.110027

$BIC
[1] 5.14702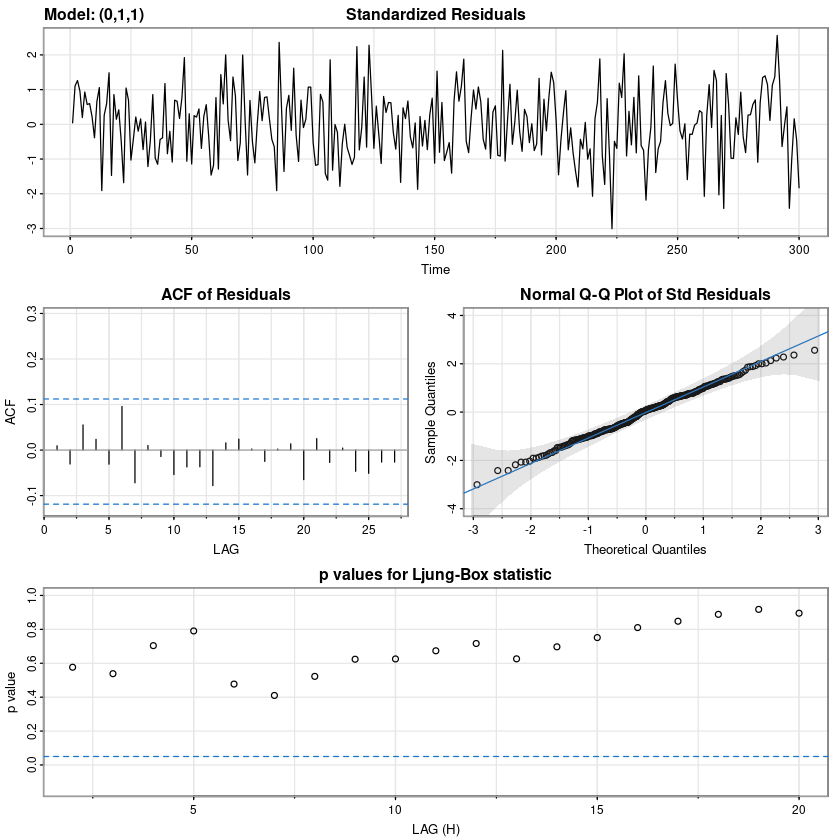

\((1-B)\hat Z_n (l) = \hat \mu - \hat \theta \hat \epsilon_n: l=1\)

\(\hat \mu: l \geq 2\)

- 원데이터를예측하는 거니까 원데이터 넣어주기(차분데이터X)

fore_fit <- forecast::forecast(fit, 25)
fore_fit
    Point Forecast     Lo 80    Hi 80     Lo 95    Hi 95
301       129.0191 125.07348 132.9647 122.98480 135.0534
302       129.0191 121.03051 137.0077 116.80160 141.2366
303       129.0191 118.43291 139.6053 112.82893 145.2093
304       129.0191 116.35746 141.6807 109.65480 148.3834
305       129.0191 114.57726 143.4609 106.93221 151.1060
306       129.0191 112.99361 145.0446 104.51022 153.5280
307       129.0191 111.55296 146.4852 102.30694 155.7313
308       129.0191 110.22240 147.8158 100.27203 157.7662
309       129.0191 108.98000 149.0582  98.37194 159.6663
310       129.0191 107.81025 150.2279  96.58297 161.4552
311       129.0191 106.70173 151.3365  94.88763 163.1506
312       129.0191 105.64572 152.3925  93.27261 164.7656
313       129.0191 104.63541 153.4028  91.72746 166.3107
314       129.0191 103.66532 154.3729  90.24384 167.7944
315       129.0191 102.73101 155.3072  88.81493 169.2233
316       129.0191 101.82878 156.2094  87.43509 170.6031
317       129.0191 100.95554 157.0827  86.09959 171.9386
318       129.0191 100.10867 157.9295  84.80441 173.2338
319       129.0191  99.28591 158.7523  83.54611 174.4921
320       129.0191  98.48531 159.5529  82.32170 175.7165
321       129.0191  97.70517 160.3330  81.12858 176.9096
322       129.0191  96.94400 161.0942  79.96448 178.0737
323       129.0191  96.20049 161.8377  78.82736 179.2108
324       129.0191  95.47344 162.5648  77.71544 180.3228
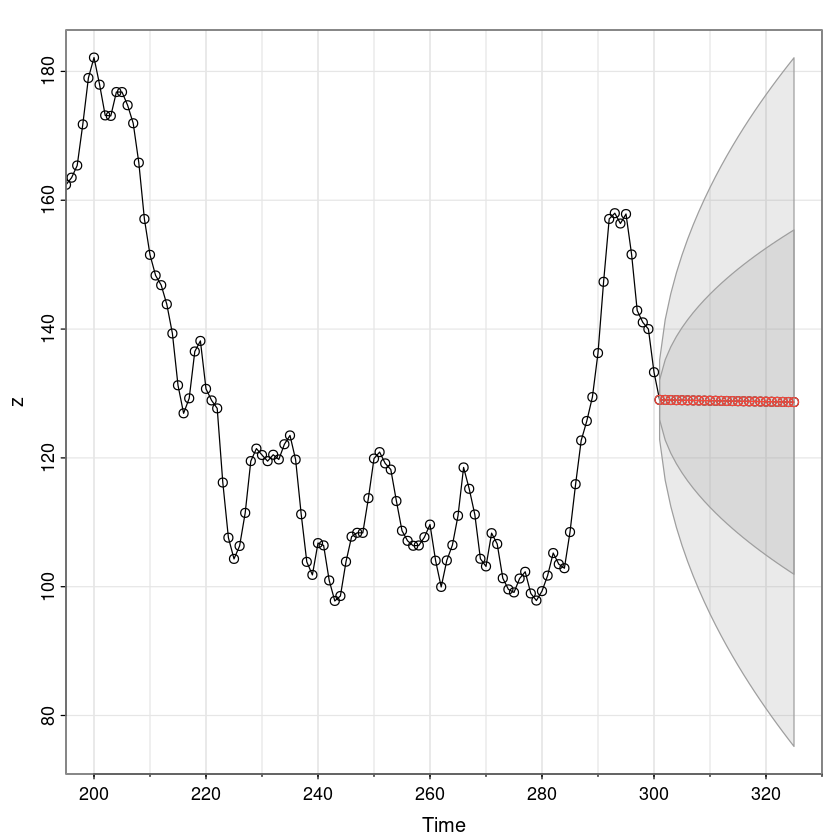
325       129.0191  94.76183 163.2764  76.62712 181.4111
plot(fore_fit)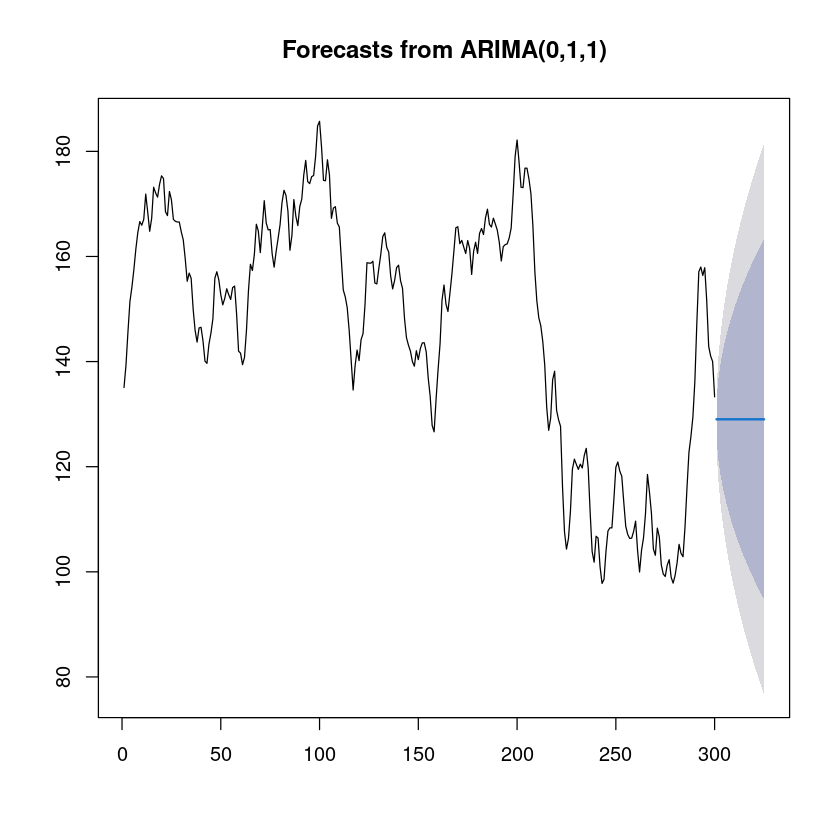

  • 평균으로 거의 예측이 됨.
astsa::sarima.for(z, 25, 0,1,1)
$pred
A Time Series:
  1. 129.010634626429
  2. 128.995997383896
  3. 128.981360141362
  4. 128.966722898829
  5. 128.952085656296
  6. 128.937448413762
  7. 128.922811171229
  8. 128.908173928696
  9. 128.893536686162
  10. 128.878899443629
  11. 128.864262201096
  12. 128.849624958562
  13. 128.834987716029
  14. 128.820350473496
  15. 128.805713230962
  16. 128.791075988429
  17. 128.776438745896
  18. 128.761801503362
  19. 128.747164260829
  20. 128.732527018296
  21. 128.717889775762
  22. 128.703252533229
  23. 128.688615290696
  24. 128.673978048162
  25. 128.659340805629
$se
A Time Series:
  1. 3.07876798320946
  2. 6.23357705966339
  3. 8.26051775756748
  4. 9.88002147201177
  5. 11.2691390510429
  6. 12.5048856698518
  7. 13.6290438505565
  8. 14.6672937839507
  9. 15.6367572600282
  10. 16.5495271314128
  11. 17.4145203476207
  12. 18.2385358404128
  13. 19.0268983354184
  14. 19.7838704739663
  15. 20.5129276700085
  16. 21.2169477602064
  17. 21.898345666366
  18. 22.5591713852255
  19. 23.2011828201129
  20. 23.8259009256026
  21. 24.434652147738
  22. 25.0286015639165
  23. 25.6087790983797
  24. 26.1761005035879
  25. 26.7313843307499

astsa::sarima.for(lag_z, 25, 0,0,1)
$pred
A Time Series:
  1. -4.29136464101854
  2. -0.014636625581003
  3. -0.014636625581003
  4. -0.014636625581003
  5. -0.014636625581003
  6. -0.014636625581003
  7. -0.014636625581003
  8. -0.014636625581003
  9. -0.014636625581003
  10. -0.014636625581003
  11. -0.014636625581003
  12. -0.014636625581003
  13. -0.014636625581003
  14. -0.014636625581003
  15. -0.014636625581003
  16. -0.014636625581003
  17. -0.014636625581003
  18. -0.014636625581003
  19. -0.014636625581003
  20. -0.014636625581003
  21. -0.014636625581003
  22. -0.014636625581003
  23. -0.014636625581003
  24. -0.014636625581003
  25. -0.014636625581003
$se
A Time Series:
  1. 3.07876823197791
  2. 3.86796612789283
  3. 3.86796612789283
  4. 3.86796612789283
  5. 3.86796612789283
  6. 3.86796612789283
  7. 3.86796612789283
  8. 3.86796612789283
  9. 3.86796612789283
  10. 3.86796612789283
  11. 3.86796612789283
  12. 3.86796612789283
  13. 3.86796612789283
  14. 3.86796612789283
  15. 3.86796612789283
  16. 3.86796612789283
  17. 3.86796612789283
  18. 3.86796612789283
  19. 3.86796612789283
  20. 3.86796612789283
  21. 3.86796612789283
  22. 3.86796612789283
  23. 3.86796612789283
  24. 3.86796612789283
  25. 3.86796612789283

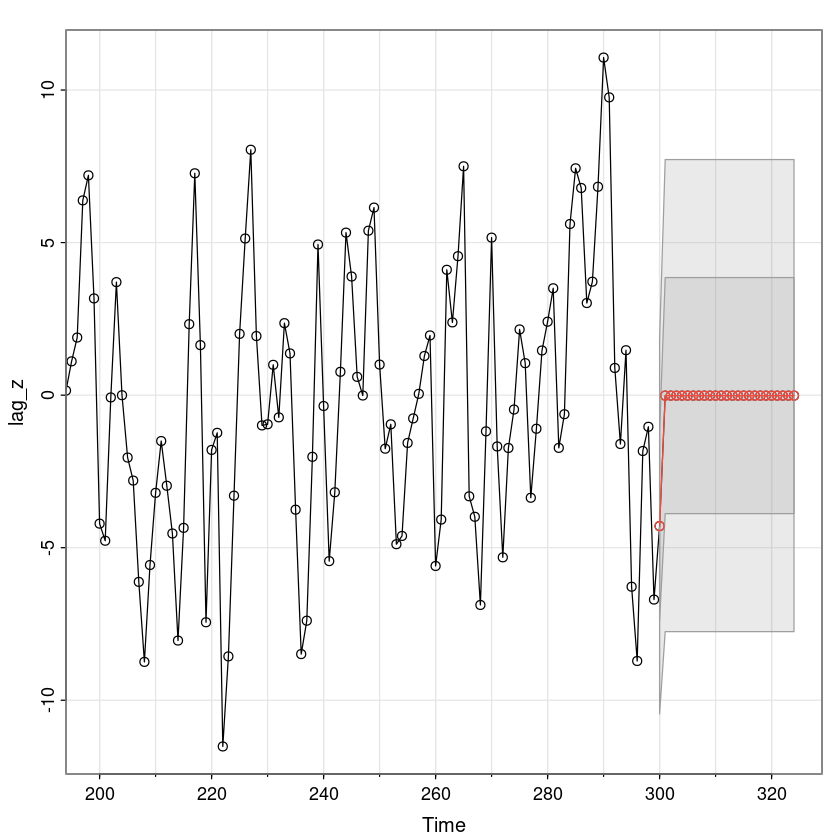
fore_diff_z <- astsa::sarima.for(lag_z, 25, 0,0,1, plot=F)$pred
fore_diff_z
A Time Series:
  1. -4.29136464101854
  2. -0.014636625581003
  3. -0.014636625581003
  4. -0.014636625581003
  5. -0.014636625581003
  6. -0.014636625581003
  7. -0.014636625581003
  8. -0.014636625581003
  9. -0.014636625581003
  10. -0.014636625581003
  11. -0.014636625581003
  12. -0.014636625581003
  13. -0.014636625581003
  14. -0.014636625581003
  15. -0.014636625581003
  16. -0.014636625581003
  17. -0.014636625581003
  18. -0.014636625581003
  19. -0.014636625581003
  20. -0.014636625581003
  21. -0.014636625581003
  22. -0.014636625581003
  23. -0.014636625581003
  24. -0.014636625581003
  25. -0.014636625581003
fore_diff_z_ <- forecast::forecast(fit1, 25)
fore_diff_z_$mean  # 차분한 값에 대한 예측
A Time Series:
  1. -4.28290139590614
  2. 0
  3. 0
  4. 0
  5. 0
  6. 0
  7. 0
  8. 0
  9. 0
  10. 0
  11. 0
  12. 0
  13. 0
  14. 0
  15. 0
  16. 0
  17. 0
  18. 0
  19. 0
  20. 0
  21. 0
  22. 0
  23. 0
  24. 0
  25. 0
fore_z <- astsa::sarima.for(z, 25, 0,1,1, plot=F)$pred
fore_z
A Time Series:
  1. 129.010634626429
  2. 128.995997383896
  3. 128.981360141362
  4. 128.966722898829
  5. 128.952085656296
  6. 128.937448413762
  7. 128.922811171229
  8. 128.908173928696
  9. 128.893536686162
  10. 128.878899443629
  11. 128.864262201096
  12. 128.849624958562
  13. 128.834987716029
  14. 128.820350473496
  15. 128.805713230962
  16. 128.791075988429
  17. 128.776438745896
  18. 128.761801503362
  19. 128.747164260829
  20. 128.732527018296
  21. 128.717889775762
  22. 128.703252533229
  23. 128.688615290696
  24. 128.673978048162
  25. 128.659340805629
fore_z_ <- forecast::forecast(fit,25)
fore_z_$mean
A Time Series:
  1. 129.01909823039
  2. 129.01909823039
  3. 129.01909823039
  4. 129.01909823039
  5. 129.01909823039
  6. 129.01909823039
  7. 129.01909823039
  8. 129.01909823039
  9. 129.01909823039
  10. 129.01909823039
  11. 129.01909823039
  12. 129.01909823039
  13. 129.01909823039
  14. 129.01909823039
  15. 129.01909823039
  16. 129.01909823039
  17. 129.01909823039
  18. 129.01909823039
  19. 129.01909823039
  20. 129.01909823039
  21. 129.01909823039
  22. 129.01909823039
  23. 129.01909823039
  24. 129.01909823039
  25. 129.01909823039

- 차분한 값에.. 원래데이터의 예측값을 알고 싶다면?

\(\widehat{▽Z_t} = \hat Z_t − \hat Z_{t−1}\)

\(\hat Z_t = \widehat{▽Z_t} + \hat Z_{t−1}\)

\(\hat Z_{300}(1) = \widehat{▽Z_{300}(1)} + Z_{300}\)

z_300_1 <- as.numeric(fore_diff_z[1]) + z[300]
z_300_1
129.010635358981

\(\hat Z_{300}(2) = \widehat{▽Z_{300}(2)} + \hat Z_{300}(1)\)

z_300_2 <- fore_diff_z[2] + z_300_1
z_300_2
128.9959987334